Parsing with PetitParser2
TL;DR
PetitParser is a top-down parsing framework that combines ideas from scannerless parsing, parser combinators, parsing expression grammars and packrat parsers to model grammars and parsers as objects that can be reconfigured dynamically.
This tutorial introduction to PetitParser is based on the online tutorial Parsing with PetitParser2, which in turn was based on Writing Parsers with PetitParser.
For an extended example, see the PetitParser SPL case study.
PetitParser and PetitParser2
PetitParser was originally implemented in Smalltalk by Lukas Renggli as a component of the Helvetia language embedding framework.
PetitParser2 is a complete reimplementation of PetitParser by Jan Kurš. The latter is integrated into GT as a key component of its language workbench support, together with SmaCC.
In general, when we refer to “PetitParser”, we mean the version of PetitParser2 that is part of GT.
Writing Parsers with PetitParser2
PetitParser is a parsing framework that differs from many other popular parser generators. For example, it is not table-based such as SmaCC or ANTLR. Instead it uses a unique combination of four alternative parser methodologies: scannerless parsers, parser combinators, parsing expression grammars and packrat parsers. As such PetitParser2 is more powerful in what it can parse and it arguably fits better the dynamic nature of Smalltalk. Let’s have a quick look at these four parser methodologies:
- Scannerless Parsers combine what is usually done by two independent tools (scanner and parser) into one. This makes writing a grammar much simpler and avoids common problems when grammars are composed.
- Parser Combinators are building blocks for parsers modeled as a graph of composable objects; they are modular and maintainable, and can be changed, recomposed, transformed and reflected upon.
- Parsing Expression Grammars (PEGs) provide ordered choice. Unlike in parser combinators, the ordered choice of PEGs always follows the first matching alternative and ignores other alternatives. Valid input always results in exactly one parse-tree, the result of a parse is never ambiguous.
- Packrat Parsers give linear parse time guarantees and avoid common problems with left-recursion in PEGs.
Writing a Simple Grammar
Writing grammars with PetitParser is simple as writing Smalltalk code. For example to write a grammar that can parse identifiers that start with a letter followed by zero or more letter or digits is defined as follows. In a workspace we evaluate:
identifier := #letter asPParser , #word asPParser star.
If you inspect the object identifier you’ll notice that it is an instance of a PP2SequenceNode
. This is because the #, operator created a sequence of a letter and a zero or more word character parser. If you dive further into the object (see the Tree view) you notice the following simple composition of different parser objects:
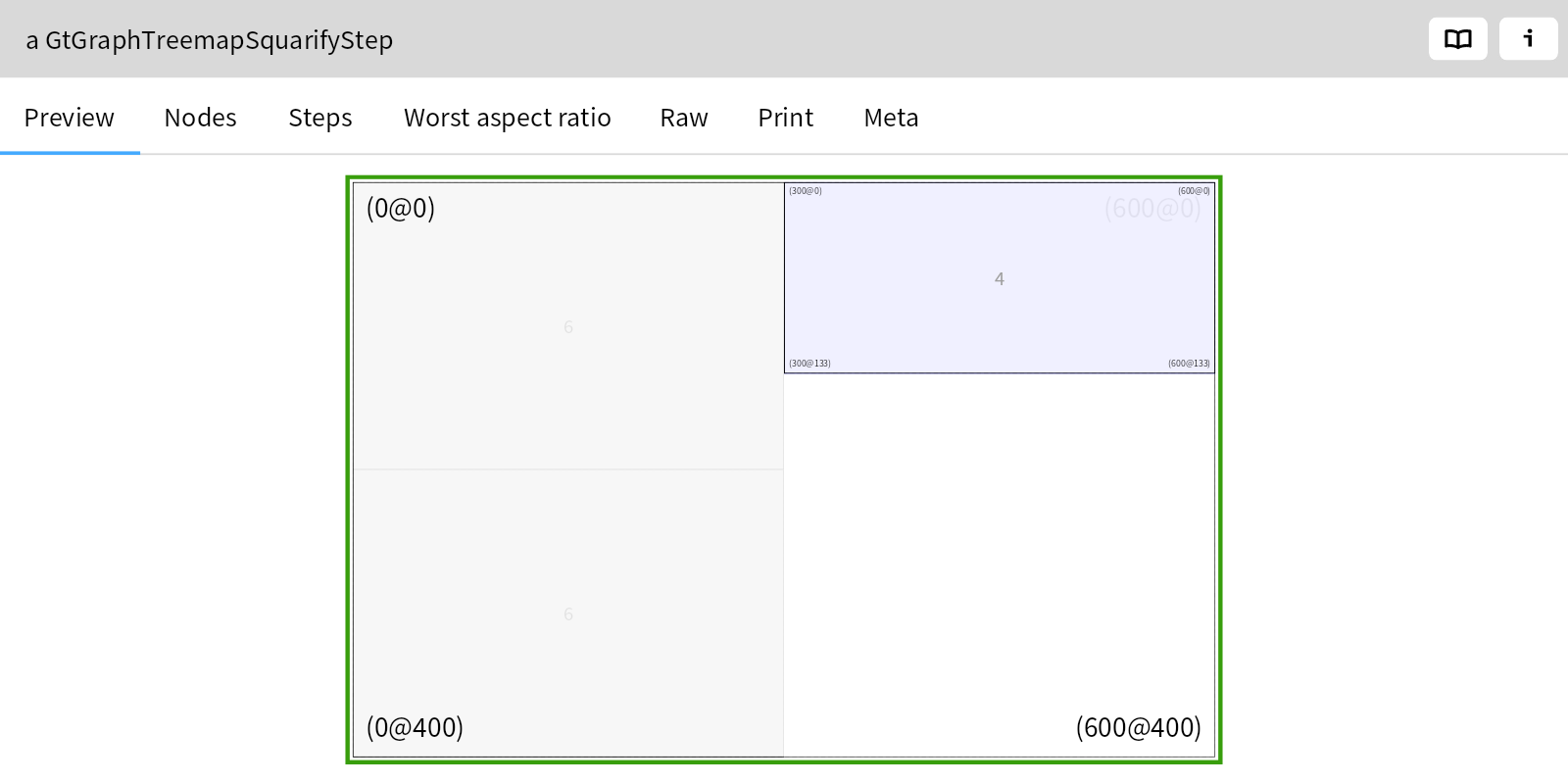
PP2SequenceNode
(this parser accepts a sequence of parsers)
PP2PredicateObjectNode
(this parser accepts a single letter)
PP2RepeatingNode
and its subclass PP2PossesiveRepeatingNode
(this parser accepts zero or more instances of another parser)
Parsing Some Input
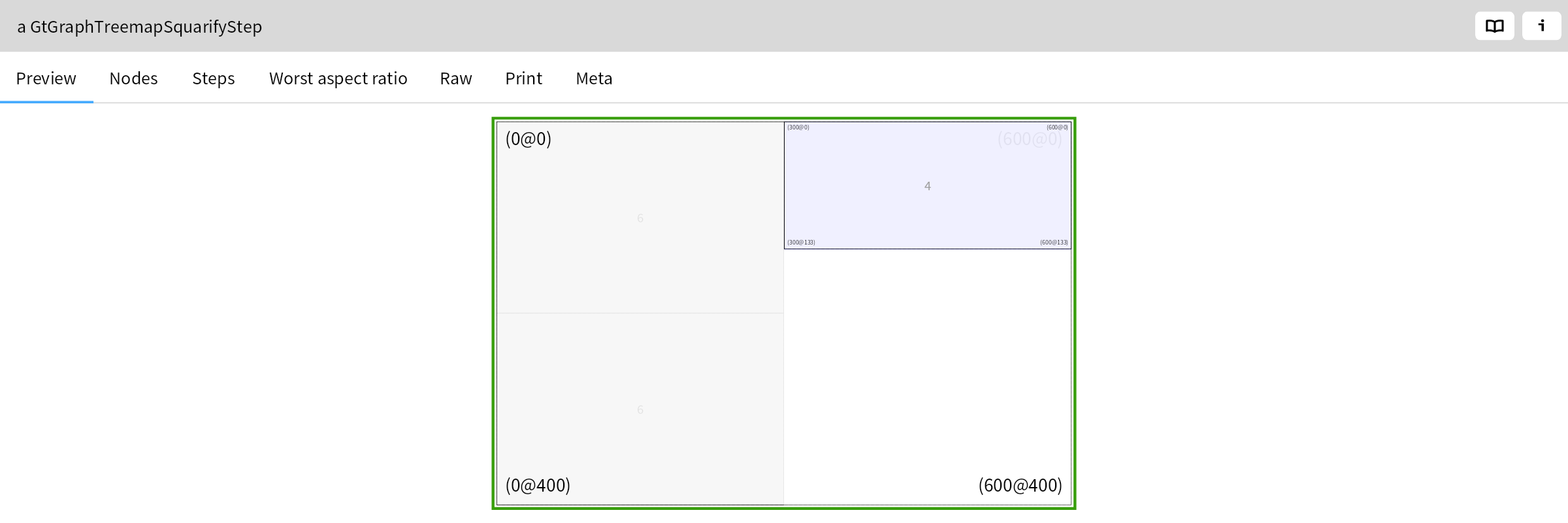
To actually parse a string (or stream) we can use the method #parse:.
identifier parse: 'yeah'.
identifier parse: 'f12'.
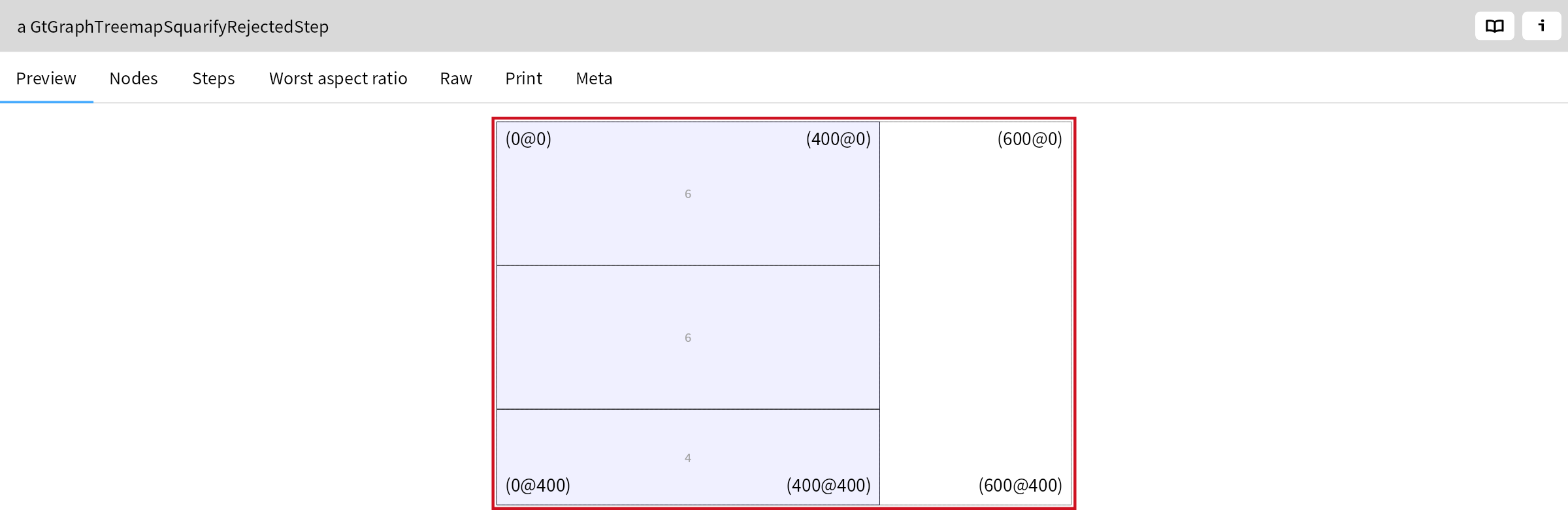
While it seems odd to get these nested arrays with characters as a return value, this is the default decomposition of the input into a parse tree. We’ll see in a while how that can be customized.
If we try to parse something invalid we get an instance of PP2Failure
as an answer:
identifier parse: '123'.
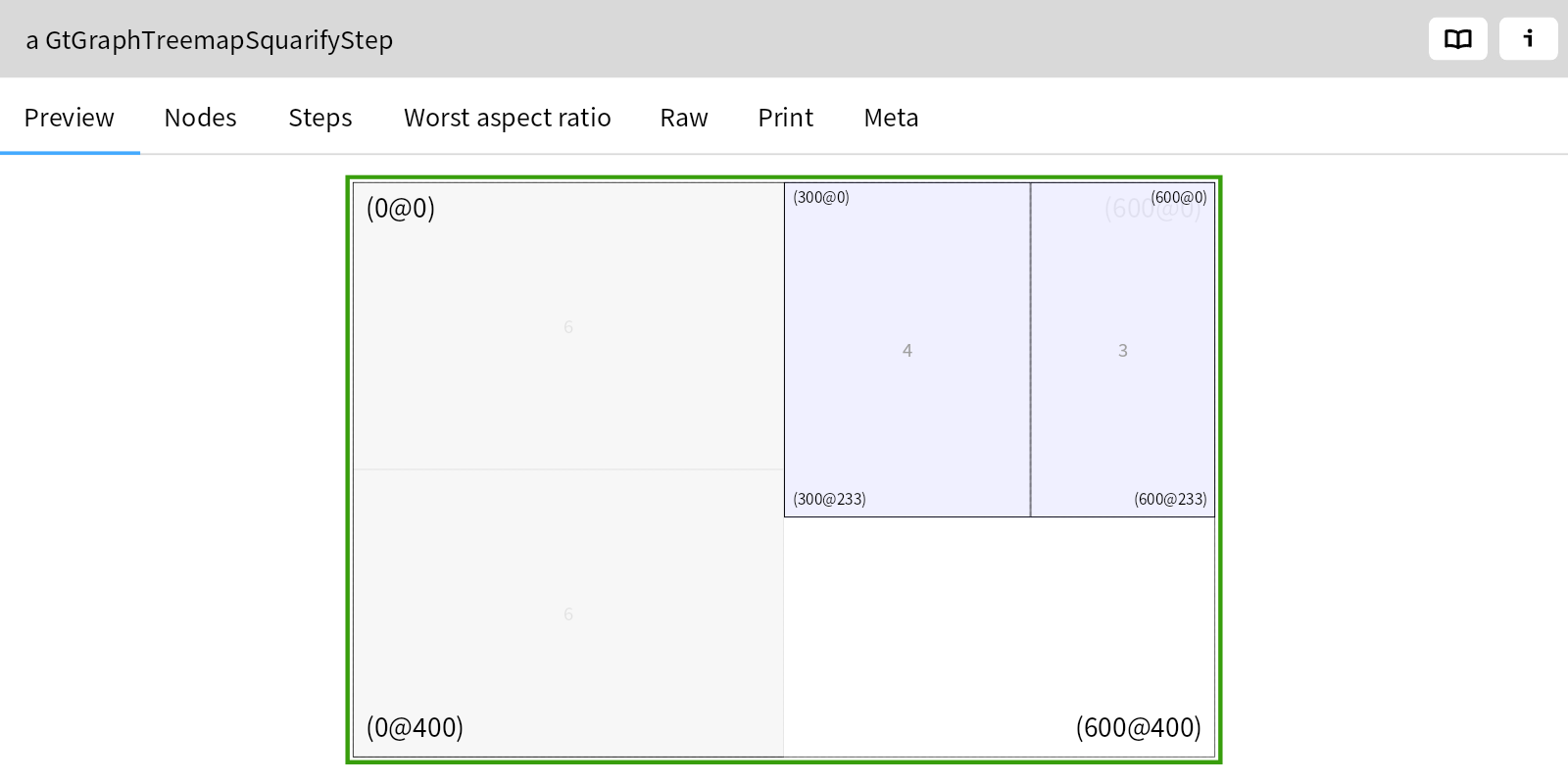
Instances of PP2Failure are the only objects in the system that answer with true when you send them the message #isPetitFailure. Alternatively you can also use #parse:onError: to throw an exception in case of an error:
identifier parse: '123' onError: [ :msg :pos | self error: msg ].
If you are only interested if a given string (or stream) matches or not you can use the following constructs:
identifier matches: 'foo'.
identifier matches: '123'.
Different Kinds of Parsers
PetitParser2 provides a large set of ready-made parsers that you can compose to consume and transform arbitrarily complex languages. The terminal parsers are the most simple ones. We’ve already seen a few of those:
$a asPParser. "Parses the character $a."
'abc' asPParser. "Parses the string 'abc'."
#any asPParser. "Parses any character."
#digit asPParser. "Parses the digits 0..9."
#letter asPParser. "Parses the letters a..z and A..Z."
The PP2NodeFactory
provides a lot of other factory methods that can be used to build more complex terminal parsers.
The next set of parsers are used to combine other parsers together:
p1 , p2 — Parses p1 followed by p2 (sequence).
p1 / p2 — Parses p1, if that doesn’t work parses p2 (ordered choice).
p star — Parses zero or more p.
p plus — Parses one or more p.
p optional — Parses p if possible.
p and — Parses p but does not consume its input.
p not — Parses p and succeeds when p fails, but does not consume its input.
p negate — Parses p and consumes any input but p
p end — Parses p and succeeds at the end of the input.
Instead of using the #word predicate we could have written our identifier parser like this:
identifier := #letter asPParser , ( #letter asPParser / #digit asPParser) star
To attach an action or transformation to a parser we can use the following methods:
p ==> aBlock — Performs the transformation given in aBlock.
p flatten — Creates a string from the result of p.
p token — Creates a token from the result of p.
p trim — Trims whitespaces before and after p.
To return a string of the parsed identifier, we can modify our parser like this:
identifier := (#letter asPParser , ( #letter asPParser / #digit asPParser) star) flatten.
identifier parse: 'howdy'
These are the basic elements to build parsers. There are a few more well-documented and tested factory methods in the operations protocol of PP2Node
. If you want, browse that protocol.
Writing a More Complicated Grammar
Now we are able to write a more complicated grammar for evaluating simple arithmetic expressions. Within a workspace we start with the grammar for a number (actually an integer):
number := #digit asPParser plus token trim ==> [ :token | token value asNumber ].
number parse: '42'.
Then we define the productions for addition and multiplication in order of precedence. Note that we instantiate the productions as PP2UnresolvedNode
upfront, because they recursively refer to each other. The method #def: resolves this recursion using the reflective facilities of the host language:
term := PP2UnresolvedNode new. prod := PP2UnresolvedNode new. prim := PP2UnresolvedNode new. term def: ((prod , $+ asPParser trim , term) ==> [ :nodes | nodes first + nodes last ]) / prod. prod def: ((prim , $* asPParser trim , prod) ==> [ :nodes | nodes first * nodes last ]) / prim. prim def: (($( asPParser trim , term , $) asPParser trim) ==> [ :nodes | nodes second ]) / number
To make sure that our parser consumes all input we wrap it with the end parser into the start production:
start := term end.
That’s it, now we can test our parser and evaluator:
start parse: '1 + 2 * 3'.
start parse: '(1 + 2) * 3'.
As an exercise we could extend the parser to also accept negative numbers and floating point numbers, not only integers. Furthermore it would be useful to add support subtraction and division as well. All these features can be added with a few lines of PetitParser2 code.
Coda: extracting a parser class
So far we have only scripted parser within Pharo snippets, but to enable testing and practical application of parsers, we should turn them into classes.
A PetitParser class is a subclass of PP2CompositeNode
, in which each component parser is
both
a method returning that parser,
and
a slot holding an instance of that parser. In addition, there must be a start method/slot.
Although you can manually produce such a class, GT provides refactoring support to automatically extract such a class.
Suppose we have a prototype of our parser that looks like this:
number := #digit asPParser plus token trim ==> [ :token | token value asNumber ]. term := PP2UnresolvedNode new. prod := PP2UnresolvedNode new. prim := PP2UnresolvedNode new. term def: ((prod , $+ asPParser trim , term) ==> [ :nodes | nodes first + nodes last ]) / prod. prod def: ((prim , $* asPParser trim , prod) ==> [ :nodes | nodes first * nodes last ]) / prim. prim def: (($( asPParser trim , term , $) asPParser trim) ==> [ :nodes | nodes second ]) / number.
After evaluating this snippet, all of the variables are defined, so we can rewrite the script recursively, without reference to PP2UnresolvedNode
or use of the def: method. Once you have a closed snippet that just defines a parser without reference to any other code, you can automatically refactor it by right-clicking within the snippet, and selecting Extract PetitParser class.
number := #digit asPParser plus token trim ==> [ :token | token value asNumber ]. term := ((prod , $+ asPParser trim , term) ==> [ :nodes | nodes first + nodes last ]) / prod. prod := ((prim , $* asPParser trim , prod) ==> [ :nodes | nodes first * nodes last ]) / prim. prim := (($( asPParser trim , term , $) asPParser trim) ==> [ :nodes | nodes second ]) / number. expression := term end.
After you give a name to the new class and evaluate the refactoring, you will have something like this.
parser := TermPParser new
Note that a start method will be automatically created equal to the last production in the grammar. TermPParser>>#start
Then you can use the new parser as follows.
parser parse: '1+2*3'